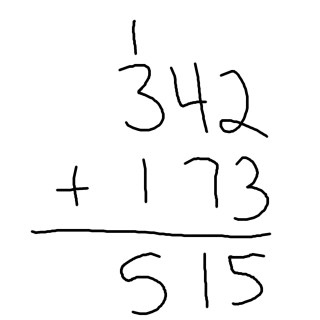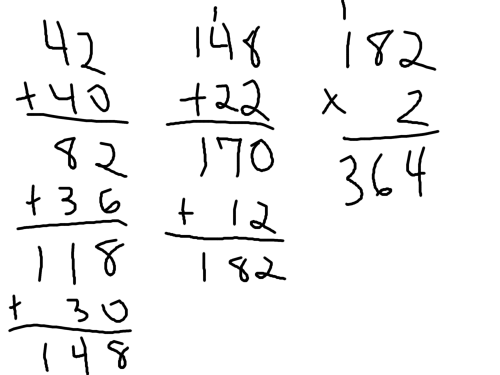Thinking about mental math for a moment…
8 minute read
April 19, 2023, 4:55 PM
I’ve mentioned before that working on the train allows me a lot of time alone with my thoughts. Sometimes that leads to my working through some of my problems and coming up with some solutions, sometimes I am mentally writing out Journal entries, sometimes it just replays traumatic experiences over and over again (though writing that letter and then mailing it to the other driver really helped me make peace with things, i.e. mentally, I think I’m going to be okay), but sometimes, I’m just doing things in my head like figuring out how many presidents have unique first names as far as the list of presidents goes, or doing math of some sort.
Funny thing about math. Growing up, I always thought that I was bad at math. I always tended to struggle in math in school, and looking back, I don’t quite understand why, because as an adult, I’m pretty sharp with math. Give me a calculator, and I can solve just about anything. I’m inclined to blame the various teaching methods used for my math struggles growing up, since it wasn’t until college, when I had Dr. Ed Parker at JMU in a summer math class to satisfy my degree requirements, when he taught us algebra in a way that made things finally fall into place. In other words, the way that we teach math kind of sucks. I also realized that I just plain don’t like division. I find it overly complicated. Flip it around and express it as multiplication, though, and I’m fine – then it all makes sense to me. Similarly, I am never doing long division by hand ever again. It’s too complicated, and besides, it’s not like I don’t always have a device with a calculator on it with me all the time these days. This, of course, is contrary to what the teachers always said growing up, i.e. that we wouldn’t have a calculator with us all the time. Clearly, these teachers never anticipated smartphones in the nineties. It’s an even stranger statement considering that calculator watches already existed at that time, even if they were not the most common of things, meaning that some people already did have a calculator on them at all times, strapped to their wrist.
But in any event, mental math, i.e. working things out in your head, is something that I always struggled with growing up, because no one really ever taught it. I’ve learned as I’ve gotten older that doing math in your head and doing it on paper are two very different processes, even if you ultimately end up with the same answer. In school, they taught us how to do math on paper. In other words, this:
Basically, start by adding three to two, which gives you five in the ones column, then add seven to four, which results in eleven in the tens column. Eleven doesn’t fit in the column, so put the last one in the tens column, and the other one gets carried over to the hundreds column, which you add three to to get four, and then add one to that four to get the final 515. And my calculator agrees with that result.
The thing is, the teachers also told us to just do math in our heads, but gave us no guidance on how to do it. If I’m doing it like I would on paper, column by column, I may have carried the one and whatever else, but by the time I did the second column, I would have forgotten what the first digit was, which meant at that point, it was an exercise in futility, because I had already dropped the ball. In other words, “Okay, two plus three is five, four plus seven is eleven, carry the one, now what was the first digit again? Oh, crap…” So doing math in my head the way that I do it on paper doesn’t work, but the educators never teach you an effective way to do it in your head with no visuals vs. on paper, where everything is written down in front of you, and therefore you don’t have to juggle all of it in your head, because the paper is holding it all for you. Subtraction is similar, because with all of the borrowing that you sometimes have to do, that’s just too much of a handful to try to do like you would on paper. Imagine trying to carry a bushel of oranges using only your arms and hands, and that’s what doing subtraction in your head the way that they teach you in school is like.
When I’m doing things in my head, I take a somewhat different approach. Recently, while I was on the train, I was trying to figure out how much stuff you ended up getting in the song “The Twelve Days of Christmas“.
First of all, for those wondering, this is what you end up with:
- 12 partridges in pear trees
- 22 turtle doves
- 30 French hens
- 36 calling birds
- 40 golden rings
- 42 geese a laying
- 42 swans a swimming
- 40 maids a milking
- 36 ladies dancing
- 30 lords a leaping
- 22 pipers piping
- 12 drummers drumming
The total is 364 different “things”. That breaks down to 184 birds, 40 pieces of jewelry, and 140 tradespeople. But anyway…
When I’m on the train, I don’t have the luxury of a calculator or a piece of paper. After all, I’m sitting in a dark box and have to continuously scan the track ahead of me to watch for hazards and such, plus there is an electronic device policy that prohibits the use of anything that I might use to calculate all of this while I’m operating. So instead of doing it column by column like they teach you in school, I’m rounding up and down and then backing out my changes.
In tackling this one, first of all, notice that the numbers mirror each other. Once we get past the sixth day of Christmas, the numbers repeat. That makes things easier, because that means that I only have to deal with half of it, and then multiply the whole thing by two. Then for me, it’s easier to work from largest to smallest, so I start with those 42 geese a laying. Then those 40 gold rings are a nice round number, so just add those in, and we now have 82 things. For the 36 calling birds, let’s round it up to 40 to make it a round number, which gives us 122 things. Then back out the four that I added to make it round, and we have 118 things. So far, so good. Then the 30 French hens are already round, so that gives us 148 things. For the 22 turtle doves, back that down to 20 for roundness, and we have 168 things. Then add that last pair of turtle doves back in, and we’ve got 170 things. Then twelve is a small enough number that I can just add it back in by itself, and we have 182 things for six days’ worth of Christmas. But since my true love sent another 182 things, including a lot of tradespeople who all want to get paid (those lords don’t leap for free, after all), we need to multiply that by two. I break that up large to small again, so 18 × 2 is 36, and then 2 × 2 is 4, and we arrive at 384. All in my head.
After coming up with that, I would first turn to my true love and say thank you, but never send me this much stuff ever again. Then I would note that this is not the way my teachers taught me to do math calculations. But I did it all in my head, and, more importantly, I got the right answer (I checked it with a calculator afterward). Here’s how it would look if I did it the way that I was taught in school:
So in other words, I was right, but it’s nothing like the way that we were taught in school. But I’m fine with that. Though I imagine that if I turned in a paper showing work the way that I do it in my head, I would probably get marked off for it, because even though I got the right answer in the end, it wasn’t the specific method that they taught us (teachers can be petty like that), and it leads us to think that there is only “one true way” of solving math problems, and that any other method is wrong, even if it still produces the right answer.
I guess what I’m trying to say through all of this is that you’re not bad at math, and it’s almost criminal that some kids are led to think that they are bad at math at a very young age and are then typecast accordingly, because that often becomes self-fulfilling. I was told that I was not good at math growing up, and then performed accordingly. But considering my experience with Ed Parker at the end of my time in college where it all finally came together, and my exploration of all sorts of things with mental math at my own pace while I’m on the train, I realize now that I was probably a lot better at math than everyone gave me credit for, as well as what I gave myself credit for. It just took me a bit longer to master the concept, and no one had the patience to help me get there. And with school and their one-size-fits-all model, and the way that math concepts tend to build on each other, if you don’t have it down yet, they were still moving on to the next concept whether you were ready or not, and so without having fully mastered the previous concept, the next concept is just built on a shaky foundation, and it all inevitably comes tumbling down in the end.
I found it quite telling in looking at my performance in algebra across three different years. In seventh grade, I had pre-algebra, which was essentially an algebra course for beginners. The pace was fairly quick, and my grades were mediocre. Based on my seventh grade performance, I was placed in the two-part version of Algebra I in eighth grade. That was the regular high school algebra course, but split across two years, which explored concepts at a slower, more thoughtful pace. I did very well in that class, getting mostly As and Bs. A confidence builder: maybe I was not as bad at math as I thought I was, because I was doing well in math for a change. But then in high school, classes were scheduled in a semester block format, where students took four classes for a semester, and then took four different classes in the next semester. Under that plan, called “4×4”, classes that would run for the entire year on a traditional schedule ran for only a single semester, with class periods that were twice as long as they would be on a traditional schedule. My first semester in high school, I had the second part of my Algebra I class. With the block schedule format, which compressed a year-long class into a single semester, I lost the slower, more thoughtful pace that I had in eighth grade because that year was squeezed into a single semester. That meant that I was back at the pace that pre-algebra had, and my performance reflected that, with my performing at pre-algebra levels again. Kind of a confidence killer, as my performance was mediocre again. Then geometry was always viewed as a different thing, and I did well at that, because it made intuitive sense, since it was something that I could easily visualize. I got all As in that class. But aside from geometry, I didn’t do particularly well in math in school.
Unfortunately, I have no idea about how to solve this problem. I just know what I have experienced, and its ups and downs over the years. I also have no dog in the fight when it comes to solving it, because I have no children, and have no interest in ever having children. I suppose that all I can say is that math is not as hard as people think it is, but schools don’t really give kids the space to play with it and truly master it, to everyone’s detriment, because when given enough time alone with it, it actually does work. And when it comes to doing things on paper vs. in your head, there are multiple ways of getting to the same answer, and there is no “one true way” about it. And regardless of how you went about it, the only thing that matters is that you got the right answer in the end.